Desvendando as parábolas
Clique no link
Boa Pesquisa!
Quadráticas
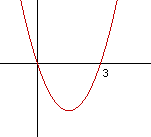
As soluções de uma equação quadrática correspondem às
intersecções com o eixo x, das abcissas (raízes) de uma
função polinomial do segundo grau. (No caso da figura,
as raízes da função são x = -1 ex=2).
Em matemática, uma equação quadrática ou equação do segundo grau é uma equação polinomial de grau dois. A forma geral deste tipo de equação é:
onde x é uma variável, e a, b e c são constantes, das quais a ≠ 0 (caso contrário, a equação torna-se linear). As constantes a, b e c, são chamadas respectivamente de coeficiente quadrático, coeficiente linear e coeficiente constante ou termo livre. A variável x representa um valor a ser determinado, e também é chamada de incógnita. O termo "quadrático" vem dequadratus, que em latim significa quadrado. Equações quadráticas podem ser resolvidas através da fatoração, do completamento de quadrados, do uso de gráficos, da aplicação do método de Newton ou do uso de uma fórmula (apresentada abaixo). Um uso frequente das equações do segundo grau é no cálculo das trajetórias de projéteis em movimento.
Introdução
A equação quadrática é, antes de tudo, um polinômio e que pertence ao segundo grau, isto é, tem como termo de maior grau (valor do expoente mais alto) um termo de expoente 2. A definição "a diferente de zero" é o que caracteriza a equação de segundo grau, visto que, a incógnita x é diretamente multiplicada pelo coeficiente a, levando-nos a crer que se a fosse igual a zero, anularia-se o x² e assim, a equação passaria a ser linear, de primeiro grau.
No século XII, o matemático Bhaskara Akaria se dispôs a resolver esta equação e publicar ao mundo suas descobertas. O maior problema dos matemáticos que tentavam achar valores para equação era o fato de haver um x de expoente 2 junto a um x de expoente 1. Sabiamente, Bhaskara aplicou princípios básicos, porém inteligentes, para finalmente achar um valor definitivo de x. A partir da descoberta de sua fórmula, diversas outras fórmulas se derivaram, como as fórmulas de Soma e Produto, Relações entre as Raízes ou os valores dos Vérticesde uma função quadrática.
Paralela à evolução dos estudos matemáticos da equação de segundo grau, cresceu também sua representação gráfica a chamada função quadrática. Nela, foi possível nitidamente, observar que há sempre um cume, valor máximo que a incógnita pode ter (chamada de Vértice), assim como a direção para a qual os valores crescem, etc. O conhecimento já guardado das funções, quando aplicados na equação quadrática, facilitaram demasiadamente os estudos de matemáticos ao longo da história, e em diversos cálculos de equações matemáticas.
Uma equação do segundo grau cujos coeficientes sejam números reais ou complexos possui duas soluções, chamadas de raízes da equação. As raízes são dadas pela seguinte fórmula:
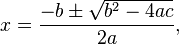
sendo a, b e c os mesmos coeficientes da equação de segundo grau, e o símbolo ± indica que uma das soluções é obtida através da soma e a outra por meio da diferença.
A fórmula acima é utilizada para determinar as raízes de uma equação quadrática, isto é, os valores que x pode assumir. No Brasil, a fórmula é conhecida como Fórmula de Bhaskara, mas em outros países é conhecida simplesmente como a fórmula geral para resolução da equação polinomial do segundo grau,[1] sem qualquer referência a Bhaskara, que foi um matemático e astrônomo indiano do século XII, e autor do livro Lilavat. A descoberta da fórmula costuma ser atribuída aos babilônios antigos, e sua formalização ao matemático persa Al-Khwarizmi[carece de fontes].
Demonstração
Por muitos tempos, muitos estudiosos tentaram achar uma solução para x dentro desta equação, visto ter sido complicado, já que havia um termo ao quadrado e o mesmo de primeiro grau, na mesma equação.[carece de fontes] Assim, a fórmula de Bhaskara utiliza um método inteligente, unindo pura e simplesmente, uma fatoração de um polinômio para conseguir pôr apenas uma incógnita x no caso e assim, achar um valor definitivo[carece de fontes]:
Se  então:
então:
 então:
então: |
Logo, tem-se, por definição de módulo, que:
Se  | Se  |
|---|---|
 |  |
Portanto,
 |
Discriminante
Na fórmula acima, a expressão que aparece sob a raiz quadrada é chamada de discriminante da equação quadrática, e é comumente denotada pela letra grega delta maiúsculo:
Dessa forma, pode-se reescrever a fórmula resumidamente como:

Uma equação quadrática com coeficientes reais tem duas raízes reais, ou então duas raízes complexas. O discriminante da equação determina o número e a natureza das raízes. Há apenas três possibilidades: (Lembrando que todo polinômio de grau n, tem n raízes; Como uma equação do 2º grau é de grau 2, logo ela possui duas raízes.)
- Se Δ > 0, a equação tem duas raízes reais distintas.
- No caso de equações quadráticas com coeficientes inteiros, se o discriminante for um quadrado perfeito, então as raízes sãonúmeros racionais — em outros casos eles podem ser irracionais quadráticos.
- Se Δ = 0 , a equação tem duas raízes reais e iguais, ou popularmente "uma única raiz", algumas vezes chamada de raiz dupla:
 .
.
- Se Δ < 0, a equação não possui qualquer raiz real. Em vez disso, ela possui duas raízes complexas distintas, que são conjugadas uma da outra:
-
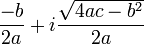
e 
- onde i é a unidade imaginária.
Assim as raízes são distintas se e somente se o discriminante é não nulo, e são reais se e somente se o discriminante é não-negativo.
Geometria
- são também as raízes da função quadrática:
uma vez que elas são os valores de x para os quais
Se a, b, e c são números reais e o domínio de f é o conjunto dos números reais, então as raízes de fsão exatamente as abcissas dos pontos nos quais o gráfico toca o eixo x.
Disto segue que, se o discriminante é positivo, o gráfico toca o eixo x em dois pontos, se for zero o gráfico toca em apenas um ponto e se for negativo, o gráfico não encosta no eixo x.
Forma fatorada da equação quadrática
O termo
é um fator do polinômio
se e somente se r é uma raiz da equação quadrática
Segue da fórmula quadrática que
No caso especial em que a quadrática possui apenas uma raiz (b2 = 4ac, isto é, discriminante nulo), o polinômio quadrático pode ser fatorado como
Relações entre coeficientes e raízes
As fórmulas de Viète fornecem uma relação simples entre as raízes de um polinômio e seus coeficientes. No caso do polinômio quadrático, elas tomam a seguinte forma
A partir de fórmula de Bhaskara, pode-se deduzir expressões bastante simples para a soma e para o produto das raízes r1 e r2 da equação:
e
Estas igualdades seguem diretamente da relação:
que pode ser comparada termo a termo com:
Em alguns casos simples, o uso dessas propriedades permite que se deduza quais são as raízes, pela simples inspeção visual e tentativa de composição de dois números que satisfaçam as relações dadas para a soma e para o produto das raízes.
A primeira das duas fórmulas fornece também uma expressão conveniente ao traçar o gráfico de uma função quadrática. Uma vez que o gráfico é simétrico com relação a uma reta vertical passando pelo vértice da parábola, quando há duas raízes reais a abscissa do vértice está localizada na média aritmética das duas raízes, isto é, seu valor é dado pela expressão:
A outra coordenada pode ser obtida através da substituição do resultado anterior na expressão quadrática, resultando em
Assim, o gráfico da função f(x) = ax2 + bx + c será sempre uma parábola com vértice em
Para um estudo mais detalhado do gráfico, ver função quadrática.
Em termos práticos, as fórmulas de Viète fornecem um método útil para a busca de raízes de uma quadrática no caso em que uma raiz é bem menor do que a outra. Se |x 1| << |x 2|, então x 1 + x 2 ≈ x 1, e tem-se a estimativa:
Da segunda fórmula de Viète resulta:
Estas fórmulas são mais fáceis de avaliar do que a fórmula de Bhaskara sob a condição de que uma raiz é grande e uma pequena, porque a fórmula de resolução de equações quadráticas avalia a raíz menor como a diferença entre dois numeros praticamente iguais (no caso em que b é grande), o que causa erros de arredondamento em avaliações numéricas. A figura ao lado mostra a diferença entre (i) um calculo direto usando a fórmula de Bhaskara (preciso quando as raízes têm valores próximos) e (ii) uma avaliação baseada na aproximação das fórmulas de Viète dadas acima (precisa quando as raízes estão bem separadas). Conforme o coeficiente linear b aumenta, inicialmente a fórmula quadrática é precisa, e a a fórmula aproximada melhora sua precisão, levando a pequenas diferenças entre os métodos ao aumentar b. No entanto, em algum ponto a fórmula de Bhaskara começa a perder precisão devido aos erros de arredondamento, enquanto o método aproximado continua a melhorar. Consequentemente a diferença entre os métodos começa a aumentar ao paço que a fórmula de Bhaskara fica cada vez pior.
Esta situação aparece com frequência em design de amplificadores, onde raízes é desejável raízes bastante separadas para garantir uma operação estável.
Outras Relações entre as Raízes
Denotando-se as raízes de uma equação do segundo grau por r1 e r2, sua soma por S = r1 + r2 e seu produto por  , verificam-se as seguintes relações entre as raízes:
, verificam-se as seguintes relações entre as raízes:
 , verificam-se as seguintes relações entre as raízes:
, verificam-se as seguintes relações entre as raízes:| Expressão envolvendo as raízes | Definição | Relação com S e P |
|---|---|---|
| Soma do inverso das raízes |  |  |
| Soma dos quadrados das raízes |  | S2 − 2P |
| Soma dos quadrados dos inversos das raízes |  |  |
| Soma dos cubos das raízes |  |  |
| Média aritmética das raízes |  |  |
| Média geométrica das raízes |  |  |
| Média harmônica das raízes |  |  |
Resolução das equações incompletas
c=0
É uma equação no formato ax2 + bx = 0. A solução é feita da seguinte forma:  . Portanto, x = 0ou
. Portanto, x = 0ou  . Nesse caso, uma das raízes será sempre zero e a outra será real (se os coeficientes o forem).
. Nesse caso, uma das raízes será sempre zero e a outra será real (se os coeficientes o forem).
 . Portanto, x = 0ou
. Portanto, x = 0ou  . Nesse caso, uma das raízes será sempre zero e a outra será real (se os coeficientes o forem).
. Nesse caso, uma das raízes será sempre zero e a outra será real (se os coeficientes o forem).É uma equação no formato ax2 + c = 0. A resolução é feita deste modo:  . Por isso,
. Por isso,  , ou a equação não terá raízes reais. No caso delas serem reais, as raízes serão simétricas.
, ou a equação não terá raízes reais. No caso delas serem reais, as raízes serão simétricas.
 . Por isso,
. Por isso,  , ou a equação não terá raízes reais. No caso delas serem reais, as raízes serão simétricas.
, ou a equação não terá raízes reais. No caso delas serem reais, as raízes serão simétricas.
Notas
- ↑ Refatti & Bisognin (2005), p. 2.
Bibliografia
- MURAKAMI, Gelson Iezzi Carlos. "Fundamentos da Matemática Elementar - Volume 1". 8ª Edição. São Paulo: Atual, 2004. ISBN 85-357-0455-8
- Refatti, Liliane Rose; Bisognin, Eleni. Aspectos Históricos e Geométricos da Equação Quadrática.
- Elon Lages Lima, Paulo Cezar Pinto Carvalho, Eduardo Wagner, Augusto César Morgado. A Matemática do Ensino Médio - Volume 1. 5ª Edição. Capítulo 6. SBM, 2001. ISBN 85-85818-10-7
Exercícios:
Questões:
01. (UNIFORM) O gráfico da função f, de R em R, definida por f(x) = x2 + 3x - 10, intercepta o eixo das abscissas nos pontos A e B. A distância AB é igual a:a) 3
b) 5
c) 7
d) 8
e) 9
02. (CEFET - BA) O gráfico da função y = ax2 + bx + c tem uma só intersecção com o eixo Ox e corta o eixo Oy em (0, 1). Então, os valores de a e b obedecem à relação:
a) b2 = 4a
b) -b2 = 4a
c) b = 2a
d) a2 = -4a
e) a2 = 4b
03. (ULBRA) Assinale a equação que representa uma parábola voltada para baixo, tangente ao eixo das abscissas:
a) y = x2
b) y = x2 - 4x + 4
c) y = -x2 + 4x - 4
d) y = -x2 + 5x - 6
e) y = x - 3
04. A solução da inequação (x - 3) (-x2 + 3x + 10) < 0 é:
a) -2 < x < 3 ou x > 5
b) 3 < x < 5 ou x < -2
c) -2 < x < 5
d) x > 6
e) x < 3
05. Os valores de x que satisfazem à inequação x2 - 2x + 8) (x2 - 5x + 6) (x2 - 16) < 0 são:
a) x < -2 ou x > 4
b) x < -2 ou 4 < x < 5
c) -4 < x < 2 ou x > 4
d) -4 < x < 2 ou 3 < x < 4
e) x < -4 ou 2 < x < 3 ou x > 4
06. (VIÇOSA) Resolvendo a inequação (x2 + 3x - 7) (3x - 5) (x2
a) incorreto porque não houve inversão do sentido da desigualdade;
b) incorreto porque nunca podemos cancelar um termo que contenha a incógnita;
c) incorreta porque foi cancelado um trinômio do segundo grau;
d) correto porque o termo independente do trinômio cancelado é 3;
e) correto, pois (x2 - 2x + 3) > 0 , " x Îℝ.
07. (UEL) A função real f, de variável real, dada por f(x) = -x2 + 12x + 20, tem um valor:
a) mínimo, igual a -16, para x = 6;
b) mínimo, igual a 16, para x = -12;
c) máximo, igual a 56, para x = 6;
d) máximo, igual a 72, para x = 12;
e) máximo, igual a 240, para x = 20.
08. (PUC - MG) O lucro de uma loja, pela venda diária de x peças, é dado por L(x) = 100 (10 - x) (x - 4). O lucro máximo, por dia, é obtido com a venda de:
a) 7 peças
b) 10 peças
c) 14 peças
d) 50 peças
e) 100 peças
09. (UE - FEIRA DE SANTANA) Considerando-se a função real f(x) = -2x2 + 4x + 12, o valor máximo desta função é:
a) 1
b) 3
c) 4
d) 12
e) 14
10. (ACAFE) Seja a função f(x) = -x2 - 2x + 3 de domínio [-2, 2]. O conjunto imagem é:
a) [0, 3]
b) [-5, 4]
c) ]-¥, 4]
d) [-3, 1]
e) [-5, 3]
Resolução:
| 01. D | 02. A | 03. C | 04. A |
| 05. D | 06. E | 07. C | 08. A |
| 09. E | 10. B |
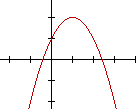
| (A) a<0, b<0 e c>0 (B) a>0, b>0 e c<0 (C) a>0, b>0 e c>0 (D) a<0, b>0 e c<0 (E) a<0, b>0 e c>0 2) Qual a função que representa o gráfico seguinte? |
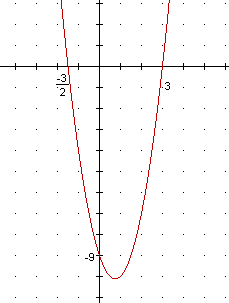
(A) 
(B)
(C)
(D)
(E)
(B)
(C)
(D)
(E)
3) O valor mínimo do polinômio
(A) 
(B)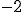
(B)
(C) 
(D) 
(E) 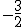
4) (UFRGS) As soluções reais da desigualdade
(A)
(B)
(C)
(D)
(E)
5) (UFRGS) O movimento de um projétil, lançado para cima verticalmente, é descrito pela equação
(A) 6,25 m, 5s
(B) 250 m, 0 s
(C) 250 m, 5s
(D) 250 m, 200 s
(E) 10.000 m , 5s
6) (UFRGS) Considere a função
(A) não intercepta o eixo das abscissas
(B) intercepta o eixo horizontal em dois pontos, de abscissas negativa e positiva respectivamente
(C) intercepta o eixo das abscissas em um único ponto
(D) intercepta o eixo das abscissas em dois pontos, ambos positivos.
(E) intercepta o eixo das ordenadas em dois pontos.
7) A razão entre a soma e o produto das raízes da equação
(A)
(B)
(C)
(D)
(E)
8) A solução de
(A) (0, 1)
(B) (-∞, 0)U(1, +∞)
(C) (-1, 1)
(D) (-∞, -1)U(1,+∞)
(E) R
9) (UFRGS) Para que a prábola da equação
(A)
(B)
(C)
(D)
(E)
10) O vértice da parábola que corresponde à função
(A) (-2, -2)
(B) (-2, 0)
(C) (-2, 2)
(D) (2, -2)
(E) (2, 2)
11) A figura abaixo ilustra uma ponte suspensa por estruturas metálicas em forma de arco de parábola.
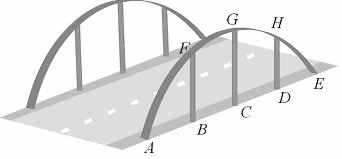
(A) 17,5m
(B) 15,0m
(C) 12,5m
(D) 10,0m
(E) 7,5m
| GABARITO | |||
| 01-E | 04-D | 07-A | 10-E |
| 02-C | 05-C | 08-A | 11 - B |
| 03-C | 06-B | 09-B | |
1) As equações abaixo definem funções do 2º grau. Para cada uma dessas funções, ache as coordenadas do vértice que a representa:
a) f(x)= x² - 4x + 5
b) f(x)= x² +4x - 6
c) f(x)= 2x² +5x - 4
d) f(x)= -x² + 6x - 2
e) f(x)= -x² - 4x +1
2) Determine, se existirem, os zeros reais das funções seguintes:
a) f(x)= 3x² - 7x + 2
b) f(x)= -x² + 3x - 4
c) f(x)= -x² + 3/2x + 1
d) f(x)= x² -4
e) f(x)= 3x²
Não existe zeros em (b)
3) Construa o gráfico das seguintes funções:
a) f(x)= x² - 16x + 63
b) f(x)= 2x² - 7x + 3
c) f(x)= 4x² - 4x +1
d) f(x)= -x² + 4x - 5
e) f(x)= -2x² +8x- 6
4) Em uma partida de vôlei, um jogador deu um saque em que a bola atingiu uma altura h em metros, num tempo t, em segundos, de acordo com a relação h(t) = -t² + 8t.
a) Em que instante a bola atingiu a altura máxima?[Nota]: observem o vértice
a) Em que instante a bola atingiu a altura máxima?[Nota]: observem o vértice
b) De quantos metros foi a altura máxima alcançada pela bola?
c) Esboce o gráfico que represente esta situação.
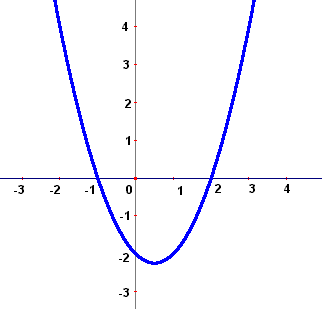
1) Esboce o gráfico da função 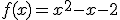 :
:
- Desenvolvimento:Vamos primeiro calcular as raízes usando Bhaskara. Os coeficientes são: a=1, b=-1 e c=-2.Colocando na fórmula de Bhaskara, temos:
Referências:
http://www.google.com.br/search?hl=pt-BR&q=exerc%C3%ADcios+fun%C3%A7%C3%A3o+2%C2%B0+grau&aq=f&aqi=&aql=&oq=
http://www.coladaweb.com/exercicios-resolvidos/exercicios-resolvidos-de-matematica/funcao-polinomial-do-segundo-grau
http://www.supletivounicanto.com.br/docs/matematica/funcao_2_grau.pdf
http://pt.scribd.com/doc/4489098/Exercicios-sobre-Funcoes-do-2-grau-
http://www.tutorbrasil.com.br/estudo_matematica_online/funcoes/funcao_segundo_grau/funcao_segundo_grau_11_01_exercicios.php
http://www.exatas.mat.br/exercicios/funcao2.htm
http://www.exatas.mat.br/exercicios/funcao2.htm
http://www.profcardy.com/exercicios/home.php?id=147&frente=1
http://www.matematica.tv/estudo_matematica_online/funcoes/funcao_segundo_grau/funcao_segundo_grau_05_exercicios_resolvidos.php
http://pessoal.sercomtel.com.br/matematica/medio/funcoes/funcoes-a.htm
http://pt.wikipedia.org/wiki/Equa%C3%A7%C3%A3o_quadr%C3%A1tica
http://www.mundoeducacao.com.br/matematica/funcao-2-grau.htm
1.Faça o gráfico das seguintes funções do 2º grau
:
:
a)y = x²
b)y = x² + 4x + 5
c) y = x² + 6x
b)y = x² + 4x + 5
c) y = x² + 6x
2.Determine as raízes das funções abaixo.
a) y = x² - 4x + 3
b) y = x²+ 8x - 12
3.A função f(x) = x2 - 2x + 1 tem mínimo no ponto em que x vale:
a. 0
b. 1
c. 2
d. 3
e. 4
4.O valor máximo da função f(x) = - x2 + 2x + 2 é:
a. 2
b. 3
c. 4
d. 5
e. 6
5.O maior valor que y pode de assumir na expressão y= - x2 +2x é:
a. 1
b. 2
c. 3
d. 4
e. 5
6.Se x e y são as coordenadas do vértice da parábola y= 3x2 -5x + 9, então x + y é igual
a:
a. 5/6
b. 31 /14
c. 83/12d. 89/18e. 93/12
que:
a.vértice do gráfico de f é o ponto (1; 4);
b.f possui dois zeros reais e distintos;
c.f atinge um máximo para x = 1;
d.gráfico de f é tangente ao eixo das abscissas.
b.f possui dois zeros reais e distintos;
c.f atinge um máximo para x = 1;
d.gráfico de f é tangente ao eixo das abscissas.
e. nda
8.O custo para se produzir x unidades de um produto é dado por C = 2x2 - 100x + 5000.
O valordo customínimo é:
a. 3250
b. 3750
c. 4000
d. 4500
e. 4950





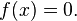
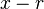


![ax^2+bx+c = a \left( x - \frac{-b + \sqrt {b^2-4ac}}{2a} \right) \left( x - \frac{-b - \sqrt {b^2-4ac}}{2a} \right) = a \left [(x - r_1)(x - r_2)\right ].](http://upload.wikimedia.org/math/7/a/0/7a02741b078e8e604d8b697b6bd7b2f6.png)
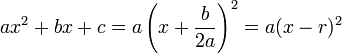




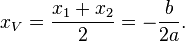
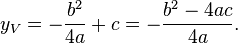




Nenhum comentário:
Postar um comentário